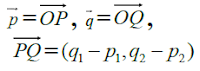MATHEMATIC is the way you think! SCIENCE is the way you life! INFORMATION is Everything you need!
Translate
Sabtu, 30 Juni 2012
TITIK DAN GARIS
1. Titik, garis, sinar dan ruas garis
Geometri dibangun atas dasar unsur-unsur yang tidak didefinisikan yaitu: titik, garis, dan bidang. Titik dipahami secara intuisi sebagai sebuah noktah yang sangat kecil, biasanya diilustrasikan dengan sebuah noktah dengan menekan ujung pensil pada kertas atau kapur tulis di papan tulis. Bidang yang dimaksud di sini adalah bidang datar yang tiada bertepi, seperti permukaan lantai yang rata tetapi tidak memiliki batas. Garis yang dimaksud di sini adalah garis lurus yang tidak memiliki ujung dan pangkal. Untuk menggambar garis sebuah garis menggunakan tanda panah diujung-ujungnya, sebagai tanda bahwa garis tersebut sebenarnya tidak berujung. Gambar 1.1 (i) mengilustrasikan sebuah garis AB, dan dilambangkan dengan AB. Di samping itu dikenal pula istilah ruas garis (segmen) dan sinar. Gambar 1.1 (ii) mengilustrasikan sebuah ruas garis EF, dilambangkan dengan EF .
Ruas garis memiliki dua titik ujung, E dan F merupakan titik-titik ujung EF . Gambar 1.1 (iii) mengilustrasikan sebuah sinar PQ, dilambangkan dengan PQ. Sinar memiliki hanya sebuah titik ujung yang biasa disebut titik pangkal. Titik P merupakan titik pangkal dari PQ. Jika tiga titik atau lebih terletak pada sebuah garis, maka titik-titik itu disebut kolinear seperti terlihat pada Gambar 1.1 (iv).
Himpunan titik-titik pada sebuah bidang, tidak selalu berbentuk garis, ruas garis, atau sinar. Ada bentuk lain yang merupakan himpunan titik-titik pada sebuah bidang, yang dikenal sebagai kurva. Kurva dipandang sebagai goresan pensil pada kertas mulai dari satu titik hingga sebuah titik tempat pensil diangkat. Gambar 1.2 (i) mengilustrasikan himpunankurva, Gb. 1.2 (ii) himpunan kurva tertutup, dan Gb. 1.2 (iii) himpunan kurva tertutup sederhana.
Apabila ada dua garis yang terletak pada suatu bidang yang sama maka terdapat tiga kemungkinan kedudukan dua garis itu (lihat Gambar 1.3), yaitu : (i) berpotongan, (ii) sejajar, atau (iii) berimpit.
Untuk keperluan menggambarkan garis-garis pada suatu bidang dikenal pula istilah garis horizontal dan garis vertikal. Pada papan tulis (berbentuk persegipanjang), yang dimaksud dengan garis horizontal adalah garis yang digambar sejajar dengan tepi bawah (atas). Garis yang digambar sejajar dengan tepi kiri (kanan) disebut garis vertikal. Pada Gambar 1.4, garis ƒÐ1 merupakan garis horizontal dan garis ƒÐ2 garis merupakan garis vertikal.
2. Aksioma Insidensi
1. Jika sesuatu itu garis, maka sesuatu itu himpunan titik.
2. Jika sesuatu itu bidang, maka sesuatu itu himpunan titik.
3. Jika diberikan dua titik yang berbeda, maka terdapat tepat sebuah garis yang melaluinya.
4. Jika diberikan tiga titik yang berbeda dan tidak segaris (kolinear), maka terdapat tepat sebuah bidang
yang memuatnya.
5. Jika dua titik yang berbeda terletak pada sebuah bidang, maka garis yang melalui titik itu terletak pada
bidang tersebut.
6. Jika dua buah bidang berpotongan maka perpotongannya meruapakan sebuah garis.
Teorema-teorema:
1. Jika dua garis yang berbeda berpotongan, maka perpotongannya tepat di satu titik.
2. Jika sebuah garis memotong sebuah bidang yang tidak memuat garis itu, maka perpotongannya sebuah
titik.
3. Jika sebuah titik terletak di luar sebuah garis, maka terdapat tepat sebuah bidang yang memuat titik dan
garis itu.
3. Jarak
Dalam keseharian, sering kita mendengar ungkapan: “Jarak dari Bandung ke Jakarta.adalah 180 km.”. Apakah kata jarak yang dimaksud dalam keseharian itu sama dengan kata jarak dalam matematika ?. Perhatikan kalimat di atas, kata jarak dipergunakan bila ada dua tempat yang berbeda, dalam hal ini Bandung dan Jakarta. Disamping itu jarak terkait dengan suatu bilangan, dalam hal ini bilangan 180. Demikian halnya dengan matematika, jarak terkait dengan dua titik yang berbeda, misal titik A dan B. Jarak titik A ke B dinyatakan dengan bilangan. Akan tetapi ada sedikit perbedaan yaitu: Pada kalimat “Jarak dari Bandung ke Jakarta.adalah 180 km.”yang 180 km itu panjang lintasan yang ditempuh kereta-api atau panjang lintasan yang ditempuh sebuah mobil ? Hal ini menghasilkan tafsiran yang berbeda, sehingga bilangan yang menyatakan jarak Bandung Jakarta itu bisa berbeda. Dalam matematika haruslah jawabnya harus tunggal. Manakah jarak Bandung Jakarta menurut matematika?
Dari gambar di atas jarak Bandung Jakarta diwakili oleh ruas garis yang menghubungkan Bandung dengan Jakarta. Tentu saja jarak tersebut harus dikalikan dengan skala pada peta yang bersangkutan. Secara matematika: Jarak antara titik A ke titik B dilambangkan dengan AB bermakna bilangan yang menyatakan
panjang AB.
Definisi:
Misalkan f : L R adalah sebuah korespondensi satu-satu antara garis L dan bilangan real. f disebut sistem koordinat untuk garis L jika dan hanya jika untuk setiap titik P dan Q berlaku PQ = f(P) – f(Q). Untuk setiap titik P pada L, bilangan x = f(P) disebut koordinat P.
Teorema-teorema:
1. Jika f adalah sebuah sistem koordinat untuk sebuah garis L, dan g(P) = - g(P) untuk setiap titik P pada
garis L, maka g adalah sebuah sistem koordinat untuk L.
2. Jika f adalah sebuah sistem koordinat untuk sebuah garis L, dan a sembarang bilangan real dan untuk
setiap titik P pada garis L g(P) = f(P) + a, maka g adalah sebuah sistem koordinat untuk L.
3. Teorema Penempatan Penggaris (Ruler Placement theorem). Misalkan L adalah sebuah garis dan P, Q
adalah dua titik sembarang yang terletak pada garis L. Maka L mempunyai sistem koordinat dengan
koordinat P adalah 0 dan koordinat Q bilangan positif.
Jumat, 29 Juni 2012
HASIL KALI TITIK DAN PROYEKSI ORTOGONAL SUATU VEKTOR
Oleh: H. Karso
FPMIPA UPI
A. Hasil Kali Titik (Hasil Kali Skalar) Dua Vektor
1. Hasil Kali Skalar Dua Vektor di R2
Perkalian diantara dua vektor tidak seperti perkalian diantara dua bilangan real. Perkalian diantara dua bilangan real hasil kalinya adalah sebuah bilangan real lagi. Namun hasil kali dua vektor belum tentu demikian. Ada beberapa jenis perkalian vektor dengan notasi dan hasil yang berbeda. Ada perkalian titik (dot product), ada perkalian silang (cross product), dan ada pula perkalian bar (bar product). Khusus dalam kegiatan belajar yang ini, hanya akan dibahas tentang perkalian titik atau hasil kali skalar dari dua vektor. Hal ini disesuaikan dengan Garis-garis Besar Program Pengajaran Mata Kuliah Aljabar Linear.
Kita perhatikan dua buah vektor yang bukan merupakan vektor nol, misalnya
dan yang dimaksud dengan hasil kali skalar (scalar product) dari dua vektor, yaitu vektor u dan vektor v adalah bentuk
Apakah Anda masih ingat salah satu aturan (rumus Cosinus) yang berlaku dalam segitiga ABC? (Trigonometri). Tentunya salah satu diantaranya seperti berikut (Gambar 4. 37).
Sekarang kita perhatikan ruas kiri dan ruas kanan dari rumus di atas, yaitu :
Ruas kanan :
Ruas kiri :
Kombinasi bentuk u1v1 + u2v2 diberi nama dan lambang yang khusus, yaitu sebagai perkalian titik (dot product) atau hasil kali skalar (scalar product), dan diberi lambang u . v. Karena penulisan ini, maka perkalian titik itu adalah :
Kita sudah mengetahui, bahwa jika (teta) sudut lancip, maka tentunya Cos (teta) adalah positif, berarti u . v positif. Sedangkan jika (teta) sudut tumpul, maka Cos (teta) adalah negatif, berarti u . v negatif. Demikian pula sebaliknya jika u . v positif, maka Cos (teta) adalah positif dan (teta) adalah sudut lancip. Sedangkan jika u . v negatif, maka Cos (teta) adalah negatif dan (teta) adalah sudut tumpul.
Tentunya besar sudut dapat kita cari (pakai kalkulator atau daftar matematika)
c) Sudut diantara u dan v ( ).
Karena u . v positif dan Cos juga positif, maka adalah sudut lancip.
Sekarang bagaimana jika kedua vektor itu saling tegak lurus ? Karena kedua vektor u dan v saling tegak lurus, maka sudut diantara keduanya adalah 90o atau
Kamis, 28 Juni 2012
Vektor dan Operasinya
Tujuan:
1. Mengingat kembali definisi vektor secara geometri dan aljabar.2. Mahir menghitung perkalian titik, panjang vektor, sudut antara dua vektor, vektor proyeksi.
3. Mahir menghitung perkalian silang dan memahami arti geometris serta penggunaannya.
4. Mahir menghitung perkalian tripel skalar dan memahami arti geometris serta penggunaannya.
Skalar: besaran saja
Vektor: besaran dan arah
Vektor secara geometri

Vektor pada sistem koordinat (aljabar)
Vektor Posisi (pada koordinat Cartesius):
Perkalian Titik
Sifat operasi perkalian titik

Rabu, 27 Juni 2012
KORELASI SPEARMAN
Korelasi spearman untuk
mengetahui hubungan antara dua variable (bebas dan terikat) berskala ordinal
(non-parametrik), misalnya skala Likert dengan pilihan 5 opsi (sangat setuju
diberi nilai 5, setuju diberi nilai 4, netral diberi nilai 3, tidak setuju
diberi nilai 2, sangat tidak setuju diberi nilai 1).
Misalnya:
Setiap sekolah pasti memiliki
kepala sekolah dan guru. Setiap kepala sekolah memiliki gaya kepemimpinan
sendiri-sendiri. Setiap guru juga berhak menilai dan bersikap atas gaya kepemimpinan
kepala sekolah. Penelitian untuk mengetahui hubungan antara sikap guru terhadap
kepemimpinan kepala sekolah dengan motivasi kinerja guru. Untuk itu disebarkan
angket model skala Likert kepada 25 guru. Masalah penelitian adalah apakah ada
hubungan antara sikap guru terhadap kepemimpinan kepala sekolah dengan motivasi
kinerja. Jika ada berapa hubungan kedua variable tersebut dan berapa sumbangan
variable bebas kepada variable terikat.
5 = sangat setuju
4 = setuju
3 = netral
2 = tidak setuju
1 = sangat tidak setuju
Sementara minat mahasiswa
diklasifikasikan sbb.
5 = sangat termotivasi
4 = termotivasi
3 = netral
2 = tidak termotivasi
1 = sangat tidak termotivasi
Dari angket diperoleh data
sebagai berikut.
Responden
|
X
|
Y
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
3
4
3
5
2
3
4
1
4
5
4
3
3
4
3
1
2
3
4
5
4
5
2
2
3
|
4
3
4
5
3
3
5
3
4
5
4
3
3
4
5
1
2
3
5
4
4
5
3
2
4
|
Penyelesaian
Tahap I: Merumuskan masalah
Tahap I: Merumuskan masalah
1. Apakah ada hubungan antara sikap guru terhadap gaya
kepemimpinan kepala sekolah dan motivasi kinerja?
2. Berapa besar hubungan antara sikap guru terhadap gaya
kepemimpinan kepala sekolah dan motivasi kinerja?
Tahap II: Membaut desain
variabel
1. Masukkan data, klik dua kali pada value sampai muncul
kotak dialog.
2. Isikan angka 5 pada
value dan kata sangat setuju pada value label kemudian klik add;
3. Isikan angka 4
pada value dan kata setuju pada value label kemudian klik add;
4. dst. Juga pada data motivasi.
Tahap III: Memasukkan data ke SPSS
Masukkan data dari 1 s.d 25.
Tahap IV: Analisis data di
SPSS
1. Analyse
2. Coorelate
3. Bivariate
4. Pindahkan variable sikap dan motivasi ke kolom
variable.
5. Correlation coefficient: pilih spearman.
6. Test of significance: pilih two tailed.
7. Cek flag significant correlation
8. Option: Missing values, pilihan: ekclude case pairwise
tekan continue.
9. Klik OK: proses
Tahap V: Penafsiran
1. Korelasi berkisar 0 s.d 1
2. Besar kecilnya korelasi menentukan kuat lemahnya
hubungan kedua varaiabel. Patokan sbb.:
0 –
0,25 korelasi sangat lemah
>
0,25 – 0,5 korelasi cukup
>
0,5 – 0,75 korelasi kuat
>
0,75 – 1 korelasi sangat kuat
3. Korelasi dapat positif dan negative.
a. Korelasi positif menunjukkan arah yang sama pada
hubungan antarvaribel. Korelasi positif
berarti jika variable 1 besar maka variable 2 semakin besar pula.
b. Korelasi negative menunjukkan arah yang berlawanan.
Korelasi negative berarti jika variable 1 naik maka variable 2 justru turun,
atau sebaliknya.
4. Hubungan siginifikan sbb:
a. Jika probabilitas < 0,05 maka hubungan kedua
variable signifikan
b. Jika probabilitas > 0,05 maka hubungan kedua
variable tidak signifikan.
5. Menentukan hipotesis sbb:
a. H0 : tidak ada hubungan yang signifikan antara X dan Y
b. H1 : ada hubungan signifikan antara X dan Y
c. Jika probabilitas < 0,05, H0 ditolak dan H1 diterima
Jika
probabilitas > 0.05, H0 diterima dan H1 ditolak.
Tahap VI: Menghitung sumbangan
atau peranan
Hitunglah peranan sikap guru
terhadap motivasi kinerja guru dengan rumus koefisien dterminasi (KD).
KD = r2 x 100%
Tahap VII: Membuat simpulan
1. Berdasarkan perhitungan statistic diperoleh angka
korelasi …… pada ts ………. Artinya……. Dengan demikian Ho……………, Hi ………………
Artinya……
2. Sumbangan atau peranan sikap guru tentang gaya
kepemimpinan kepala sekolah terhadap
motivasi kinerja ……….. %. Artinya kinerja guru ditentukan …….. % oleh variable
sikap kepada gaya kepemimpinan kepala sekolah, sedangkan sisanya ………..
ditentukan oleh variable lain.
Selasa, 26 Juni 2012
Uji Autokorelasi dengan SPSS
Autokorelasi terjadi dalam regresi apabila dua error et-1 dan et tidak independent atau C(et-1, et) ? 0. Autokorelasi biasanya terjadi apabila pengukuran variabel dilakukan dalam intereval waktu tertentu. Hubungan antara et dengan et-1 dapat dinyatakan seperti berikut.
et = ? et-1 + vt
? menyatakan koefisien autokorelasi populasi. Apabila ?=0, maka autokorelasi tidak terjadi. Apabila autokorelasi terjadi, maka ? akan mendekati +1 atau -1. Menduga terjadi tidaknya autokorelasi dengan diagram antara grafik antara et dengan et-1 sangat sulit. Deteksi autokorelasi umumnya dilakukan dengan uji statistik Durbin-Watson dengan menggunakan formula sebagai berikut.
Nilai d berkisar antara 0 dan 4, yaitu 0=d=4. Autokorelasi tidak terjadi apabila nilai d = 2. Apabila terjadi autokorelasi positif, maka selisih antara et dengan et-1 sangat kecil dan d mendekati 0. Sebaliknya, apabila Apabila terjadi autokorelasi negatif, maka selisih antara et dengan et-1 relatif besar dan d mendekati 4.
Sebagai contoh, akan diuji autokorelasi dalam regresi antara variabel bebas insentif (x1) dan iklim kerja (x2) dengan variabel terikat kinerja (y). Data hasil penelitian adalah sebagai berikut.
Langkah- langkah yang ditempuh dalam pengujian multikolinieritas adalah sebagai berikut.
a. Entry Data
Masukkan data ke dalam form SPSS, yakni data insentif dalam variabel x1, data iklim kerja pada variabel x2, data hubungan interpersonal pada x3, dan data kinerja pada variabel y.
b. Analisis Data
Pengujian autokorelasi dilakukan dengan modul regresi dengan menu seperti berikut.
Analyze
Regression
Linier …
Apabila menu tersebut sudah dipilih, maka akan muncul kotak dialog seperti berikut.
Pindahkan variabel y ke dependent list dan variabel x1, x2, dan x3 ke independent list. Setelah itu pilih boks statistics, dan pilih Durbin-Watson, sehingga tampak kotak dialog seperti berikut. Selanjutnya pilih continue, lalu OK.
Hasil yang tampak dari uji autokorelasi adalah sebagai berikut.
Ternyata koefisien Durbin-Watson besarnya 2,067, mendekati 2. Dengan demikian, dapat disimpulkan bahwa dalam regresi antara variabel bebas insentif (x1), iklim kerja (x2), dan hubungan interpersonal (x3) terhadap kinerja (y) tidak terjadi autokorelasi.
Langganan:
Komentar (Atom)